Why Pharell Williams Will Invite Me to His Next Fashion Show
Last Tuesday, the Louis Vuitton Fashion Show took place on the Pont Neuf in Paris. It was Pharell William’s first show as the new creative director at Louis Vuitton.
When something that exiting is happening, I’ve got to go see it. To attend these kind of shows you have to be invited and my girlfriend and I were not invited (Pharell, why?). So, on Tuesday evening we took of to see whether there is a chance to get near Pont Neuf and have a glimpse at all the fashionably dressed up people. We ended up at a little restaurant which refused to close for the occasion and sat down for some desert, sparkling San Pellegrino and Lychee juice. From our seats we could see staff members running around, but the actual show was still out of reach. This was the best we could do that evening and I’m sorry to disappoint you but besides hearing the music from the show, we did not manage to get any closer to the action. We even missed a live performance of Jay-z and Pharell which happened right after the show. We didn’t know it was happening :(
All of these festivities got me thinking. There must be ways to attend these shows. Lets assume another show with 1750 invitees is taking place next year. Here are some ideas I could come up with to attend these shows.
Illegal: I could figure out who some of the invitees are going to be, show up at their place, kidnap them, take their invitation and go to the show, easy. I could hire some hackers to find some confidential documents about any of the invitees and try to bribe them for the invitation. I could threaten or bribe any of the companies or staff members working at the event, to let me in. I could hire a hacker to hack into LV’s system and send out an invitation to myself.
Less illegal: I could figure out what the invitation card looks like, make a fake invitation and fool the security at the entrance. I could be a youtuber and make videos about how I sneak into venues.
Legal: I could contact some of the 1750 people that are invited to the fashion show and ask them for their invitation.
Which option should I choose?
I refuse to go to jail, so everything that’s illegal, although movie worthy, is not an option. The less illegal stuff, is mostly dishonest. Not the way. What about the legal way? Does it work? Remember the wheel (see below) from my last post? The wheel predicts that it works. Whether Pharrell knows it or not, he will invite me to his next fashion show.
I want to attend the show. If Pharrell invites me, I can attend the show. To attend the show, all I need is to be at the show the moment it is taking place. And to be at the show the moment it is taking place, I need to have an invitation. That’s it, there is no more to it, I need an invitation. What have I done here? I have defined my existence (attend the show) at a future point in time and decorticated what it actually meant (having an invitation). My existence is now myself with an invitation.
There is 1750 invitations. I could sit at home and pray to receive an invitation but the chances of that happening are practically 0. Pharrell doesn’t even know I exist. So, the first thing I have to do is to act. Act for the survival of my existence.
My action should create properties that allow me to interact with the invitation until I’m entangled with it to the point that it’s mine. The invitations are all guarded by the people who were invited. Therefore, I need to convince one of them to give their invitation to me. How can I do this?
I could ask one of the invitees whether they wanted to give me their invitation, maybe in exchange of something else, money? Maybe that works. I could also ask multiple of the invitees whether they want to give me their invitation, in exchange of whatever they want. I could also ask all invitees that I’m able to track down whether they want to give me their invitation, in exchange of whatever they want. On top of that I could do some research to offer each of them something that I believe they want, instead of just asking (people sometimes don’t know what they want).
By choosing the option in bold I’m increasing the probability of interaction between one of the invitees and myself. Since I’m willing to give them what they want, they are more likely to give me what I want in exchange. In other words, my action increases the probability of my existence (attend the show) and their existence (whoever they might be) to win and therefore to survive. If it works I will have the invitation and the now ex-invitee will have what they want. You see how this fits into the wheel? like magic.
You might be thinking that the invitee wants to go to the show and that there is no chance the person will let go of the invitation. That’s not true. For instance, there could be a sudden dislike for Pharrell, an impossibility to travel to Paris, a death of a family member, bad mood, or simply the preference for something else instead of going to the show. The point is, their is an infinite amount of scenarios where a person doesn’t “want” to attend the show. If I put all of these scenarios together I can calculate the probability of that person attending the show.
Let’s say there is a 99,9% chance that the person attends the event. I try to lower that probability by offering the person what they want. Lets assume I got the probability down to 99%. Now, there is a 1% chance that when reaching out, the person exchanges the invitation for whatever I offer. Remember that there is 1750 people with invitations? Let’s assume that I reach out to half of them, 875. I consider the probability for each of them to be 1%. What is the probability that one of them is willing to exchange their invitation for what I offer them.
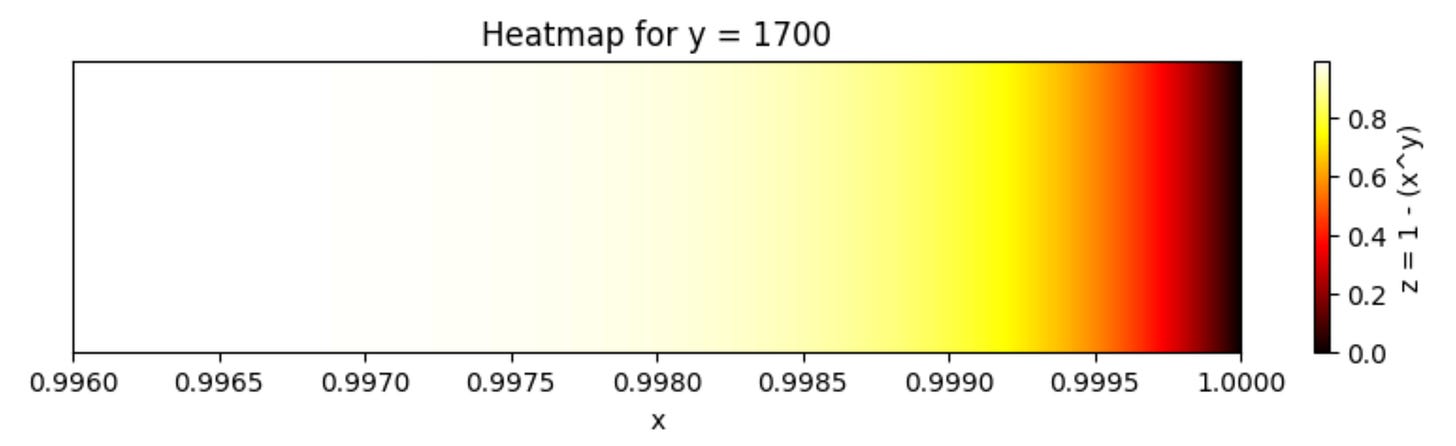
To do that I use the law of union of independent events: P(A or B or C or D etc.) = 1 - P(Not A) * P(Not B)* P(Not C) * P(Not D) etc.=> P (of one person exchanging the invitation) = 1 - (0.99^875) = 0.999848…As you can see the chances are extremely high. It is basically guaranteed that one of the invitees will trade their invitation. Their is a 0.000152% chance that none of the 875 people will trade their invitation.
The equation that I used has two variables that I can influence. One is the probability of a single event (the probability that single invitee is willing to trade their invitation) and the second, how many invitees I am interacting with. Looking at the wheel, the probability for a single event to happen can be increased by figuring out what the other person wants. I create the right properties to increase the probability of interaction. How many invitees I am interacting with is also influenced by how much I act in order for my existence (attend the show) to survive. In everyday life people call it working hard and smart. To maximize my chance of winning and therefore attend the show, the best strategy is to do both.
Consider now that I’m not smart at figuring out what people want but I work hard and reach out to almost everyone. I decrease the probability of a single event happening to 0.1% but increase the number of interactions to 1700.
P (of one person exchanging the invitation) = 1 - (0.999^1700) = 0.81747There is still a chance of more than 80% of attending the event. Now, imagine that I am very smart with people and manage to increase the probability of a single event happening from 1% as in our initial example to 2% with 875 interactions.
P (of one person exchanging the invitation) = 1 - (0.98^875) = 0.99999997In this scenario it is absolutely certain that I will get one invitation. I can predict with absolute certainty that Pharrell will invite me to his fashion show.
Conclusion
The purpose of the Hani newsletter has changed. In the description it now says “Predicting human behaviour, for the fun of it.” What did I predict in this article? I predicted with certainty that Pharrell Williams will invite me to his next fashion show. This is how predicting human behaviour works. I can not know the future in advance, it is impossible. But what I can do is to increase the probability of a future existence to exist by taking action, to the extent that it becomes a certainty.
Appendix:
Visualizations of probabilities of getting an invitation to Pharrell’s next fashion show. The function used is z=1-(x^y). That’s the same function as the one I used throughout the article, just with different notations.